Quantum synchronization of twin limit-cycle oscillators

Abstract

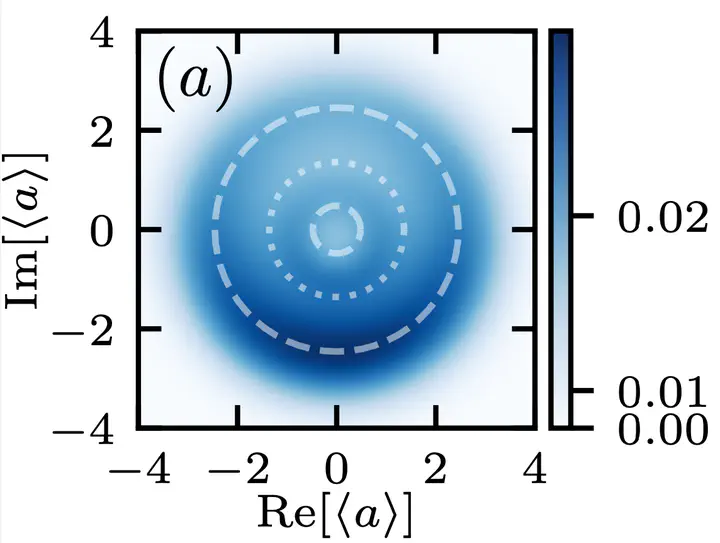
Quantum synchronization has been a subject of intensive research in the last decade. In this work, we propose a quantum Lienard system whose classical equivalent features two limit cycles to one of which the system will converge. In the quantum case, both limit cycles coexist in a single steady state. Each of these limit cycles localizes to a distinct phase if coupled to an external drive: one quantum state can thus be assigned two phases. Furthermore, coupling two such oscillators leads to the simultaneous appearance of synchronization and a synchronization blockade. To shed light on this apparent paradoxical result, we introduce finer measures of quantum synchronization.